If the underlying populations cannot be assumed to be normal, then by the central limit theorem, the sampling distribution of  1 -
1 - 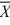 2 is approximately normal only if the sum of the sample observations is sufficiently large-that is, when n1 + n2 ≥ 30.
2 is approximately normal only if the sum of the sample observations is sufficiently large-that is, when n1 + n2 ≥ 30.
Correct Answer:
Verified
Q12: 2) multiplied by either zα/2 or tα/2,df
Q13: A common case of dependent sampling is
Q14: The difference between the two sample means
Q15: A left-tailed test determines whether μ1 is
Q16: The confidence interval for the difference μ1
Q18: There is only one type of matched-pairs
Q19: We always deal with matched-pairs sampling if
Q20: The margin of error in the confidence
Q21: Assume the competing hypotheses take the following
Q22: If the hypothesized difference d0 is _,
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents