Solved

On June 16, 1997, Two Amateur Golfers Playing Together Hit

Question 70

Multiple Choice

On June 16, 1997, two amateur golfers playing together hit back-to-back holes in one (Source: The Island Packet, June 19, 1997) . Suppose the probability of an amateur golfer getting a hole-in-one is On June 16, 1997, two amateur golfers playing together hit back-to-back holes in one (Source: The Island Packet, June 19, 1997) . Suppose the probability of an amateur golfer getting a hole-in-one is . If the golfers' shots are independent of each other, what is the probability that two amateur golfers will get back-to-back holes in one? ​ A) Pr(hole-in-one ∩ hole-in-one) = B) Pr(hole-in-one ∩ hole-in-one) = C) Pr(hole-in-one ∩ hole-in-one) = D) Pr(hole-in-one ∩ hole-in-one) = E) Pr(hole-in-one ∩ hole-in-one) = . If the golfers' shots are independent of each other, what is the probability that two amateur golfers will get back-to-back holes in one? ​


A) Pr(hole-in-one ∩ hole-in-one) = On June 16, 1997, two amateur golfers playing together hit back-to-back holes in one (Source: The Island Packet, June 19, 1997) . Suppose the probability of an amateur golfer getting a hole-in-one is . If the golfers' shots are independent of each other, what is the probability that two amateur golfers will get back-to-back holes in one? ​ A) Pr(hole-in-one ∩ hole-in-one) = B) Pr(hole-in-one ∩ hole-in-one) = C) Pr(hole-in-one ∩ hole-in-one) = D) Pr(hole-in-one ∩ hole-in-one) = E) Pr(hole-in-one ∩ hole-in-one) =
B) Pr(hole-in-one ∩ hole-in-one) = On June 16, 1997, two amateur golfers playing together hit back-to-back holes in one (Source: The Island Packet, June 19, 1997) . Suppose the probability of an amateur golfer getting a hole-in-one is . If the golfers' shots are independent of each other, what is the probability that two amateur golfers will get back-to-back holes in one? ​ A) Pr(hole-in-one ∩ hole-in-one) = B) Pr(hole-in-one ∩ hole-in-one) = C) Pr(hole-in-one ∩ hole-in-one) = D) Pr(hole-in-one ∩ hole-in-one) = E) Pr(hole-in-one ∩ hole-in-one) =
C) Pr(hole-in-one ∩ hole-in-one) = On June 16, 1997, two amateur golfers playing together hit back-to-back holes in one (Source: The Island Packet, June 19, 1997) . Suppose the probability of an amateur golfer getting a hole-in-one is . If the golfers' shots are independent of each other, what is the probability that two amateur golfers will get back-to-back holes in one? ​ A) Pr(hole-in-one ∩ hole-in-one) = B) Pr(hole-in-one ∩ hole-in-one) = C) Pr(hole-in-one ∩ hole-in-one) = D) Pr(hole-in-one ∩ hole-in-one) = E) Pr(hole-in-one ∩ hole-in-one) =
D) Pr(hole-in-one ∩ hole-in-one) = On June 16, 1997, two amateur golfers playing together hit back-to-back holes in one (Source: The Island Packet, June 19, 1997) . Suppose the probability of an amateur golfer getting a hole-in-one is . If the golfers' shots are independent of each other, what is the probability that two amateur golfers will get back-to-back holes in one? ​ A) Pr(hole-in-one ∩ hole-in-one) = B) Pr(hole-in-one ∩ hole-in-one) = C) Pr(hole-in-one ∩ hole-in-one) = D) Pr(hole-in-one ∩ hole-in-one) = E) Pr(hole-in-one ∩ hole-in-one) =
E) Pr(hole-in-one ∩ hole-in-one) = On June 16, 1997, two amateur golfers playing together hit back-to-back holes in one (Source: The Island Packet, June 19, 1997) . Suppose the probability of an amateur golfer getting a hole-in-one is . If the golfers' shots are independent of each other, what is the probability that two amateur golfers will get back-to-back holes in one? ​ A) Pr(hole-in-one ∩ hole-in-one) = 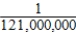B) Pr(hole-in-one ∩ hole-in-one) = 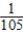C) Pr(hole-in-one ∩ hole-in-one) = D) Pr(hole-in-one ∩ hole-in-one) = 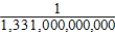E) Pr(hole-in-one ∩ hole-in-one) =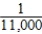

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q64: Forty-eight percent of the U.S. population is

Q66: From a deck of 52 playing cards,

Q67: Suppose the following table summarizes the opinions

Q68: A red ball and 18 white balls

Q69: A red ball and 17 white balls

Q71: A box contains 3 red balls, 5

Q73: Each computer component that the Peggos Company

Q75: Thirty-seven percent of the cars owned by

Q75: A fair die is thrown twice. What

Q77: A company estimates that 50% of the

Unlock this Answer For Free Now!

View this answer and more for free by performing one of the following actions

qr-code

Scan the QR code to install the App and get 2 free unlocks

upload documents

Unlock quizzes for free by uploading documents