Solved

Determine Whether the Function's Vertex Is a Maximum Point or a Minimum

Question 21

Multiple Choice

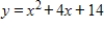
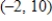Determine whether the function's vertex is a maximum point or a minimum point and find the coordinates of this point. ​ Determine whether the function's vertex is a maximum point or a minimum point and find the coordinates of this point. ​ ​ A) vertex: , a minimum point B) vertex: , a maximum point C) vertex: , a minimum point D) vertex: , a maximum point E) vertex: , a maximum point ​


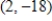A) vertex: Determine whether the function's vertex is a maximum point or a minimum point and find the coordinates of this point. ​ ​ A) vertex: , a minimum point B) vertex: , a maximum point C) vertex: , a minimum point D) vertex: , a maximum point E) vertex: , a maximum point , a minimum point
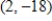B) vertex: Determine whether the function's vertex is a maximum point or a minimum point and find the coordinates of this point. ​ ​ A) vertex: , a minimum point B) vertex: , a maximum point C) vertex: , a minimum point D) vertex: , a maximum point E) vertex: , a maximum point , a maximum point
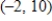C) vertex: Determine whether the function's vertex is a maximum point or a minimum point and find the coordinates of this point. ​ ​ A) vertex: , a minimum point B) vertex: , a maximum point C) vertex: , a minimum point D) vertex: , a maximum point E) vertex: , a maximum point , a minimum point
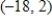D) vertex: Determine whether the function's vertex is a maximum point or a minimum point and find the coordinates of this point. ​ ​ A) vertex: , a minimum point B) vertex: , a maximum point C) vertex: , a minimum point D) vertex: , a maximum point E) vertex: , a maximum point , a maximum point
E) vertex: Determine whether the function's vertex is a maximum point or a minimum point and find the coordinates of this point. ​ ​ A) vertex: , a minimum point B) vertex: , a maximum point C) vertex: , a minimum point D) vertex: , a maximum point E) vertex: , a maximum point , a maximum point

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q16: Solve the equation below using quadratic methods.

Q17: Solve the equation Solve the</p></div><svg width=

Q18: Find the exact real solutions to the

Q19: If the profit from the sale of

Q20: Solve the equation Solve the</p></div><svg width=

Q22: Find the average rate of change of

Q23: How is the graph of

Q24: Find the vertex of the graph of

Q25: A fissure in the earth appeared after

Q26: Determine what value of x gives the

Unlock this Answer For Free Now!

View this answer and more for free by performing one of the following actions

qr-code

Scan the QR code to install the App and get 2 free unlocks

upload documents

Unlock quizzes for free by uploading documents