Multiple Choice
Suppose k, l, and m grow at constant rates given by 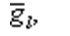 And
And
What is the growth rate of y if
A)
B)
C)
D)
E)
Correct Answer:
Verified
Related Questions
Q42: If France's per capita GDP is $5,000
Q43: Suppose x grows at a rate
Q44: Suppose k and l grow at
Q47: Suppose k0 = 100 and assume
Q47: When a lower-income economy's GDP is able
Q49: Between 1960 and 2000, which of the
Q50: In 1960, approximately _ of the world's
Q51: Suppose x grows at a rate
Q52: Between 1960 and 2010, the fraction of
Q53: Suppose k, l, and A grow
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents