Solved

A Sum of Is Invested at Interest

Question 66

Essay

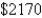A sum of A sum of is invested at interest. If is the amount of the investment at time t for the case of continuous compounding, write a differential equation and an initial condition satisfied by . is invested at A sum of is invested at interest. If is the amount of the investment at time t for the case of continuous compounding, write a differential equation and an initial condition satisfied by . interest. If A sum of is invested at interest. If is the amount of the investment at time t for the case of continuous compounding, write a differential equation and an initial condition satisfied by . is the amount of the investment at time t for the case of continuous compounding, write a differential equation and an initial condition satisfied by A sum of is invested at interest. If 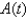is the amount of the investment at time t for the case of continuous compounding, write a differential equation and an initial condition satisfied by . .

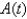Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q57: Use Euler's method with step size 0.25

Q58: Solve the differential equation. Solve</p></div><svg width=

Q59: The solution of the differential equation

Q60: Kirchhoff's Law gives us the derivative equation

Q61: For what nonzero values of k does

Q62: For what values of k does the

Q63: Newton's Law of Cooling states that the

Q64: A population is modeled by the differential

Q65: Which of the following functions are the

Q67: A function A function </p></div><svg width=

Unlock this Answer For Free Now!

View this answer and more for free by performing one of the following actions

qr-code

Scan the QR code to install the App and get 2 free unlocks

upload documents

Unlock quizzes for free by uploading documents