Intelligence Quotient (IQ) scores are assumed to be normally distributed in the population. The probability that a person selected at random from the general population will have an IQ between 100 and 120 is given by Use the graph of p (x) graphed below to answer the questions which follow: 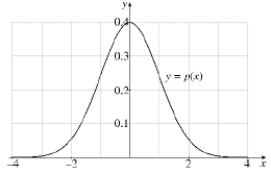
(a) Use Simpson's Rule with n = 4 to approximate
(b) The probability that a person selected from the general population will have an IQ score between 80 and 120 is given by What is the approximate value of (c) Since p (x) represents a probability distribution, the entire area of the region under the graph is exactly 1. Using this information, what is the approximate probability that a person selected at random from the general population will have an IQ score over 120?
Correct Answer:
Verified
Q28: The following table shows the speedometer
Q29: Evaluate Q30: Below is a table of values Q31: Use the Table of Integrals in Q32: Find the value of the integral Q34: Find the value of the integral Q35: Find the value of the integral Q36: Find the value of the integral Q37: Two students use Simpson's Rule to Q38: The widths (in meters) of a kidney-shaped
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents