Several authors have tried to measure the "persistence" in U.S state unemployment rates by running the following regression:  where ur is the state unemployment rate,i is the index for the i-th state,t indicates a time period,and typically k ≥ 10.
where ur is the state unemployment rate,i is the index for the i-th state,t indicates a time period,and typically k ≥ 10.
(a)Explain why finding a slope estimate of one and an intercept of zero is typically interpreted as evidence of "persistence."
(b)You collect data on the 48 contiguous U.S.states' unemployment rates and find the following estimates: 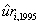 = 2.25 + 0.60 ×
= 2.25 + 0.60 × 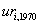 ;R2 = 0.40,SER = 0.90
;R2 = 0.40,SER = 0.90
(0.61)(0.13)
Interpret the regression results.
(c)Analyzing the accompanying figure,and interpret the observation for Maryland and for Washington.Do you find evidence of persistence? How would you test for it? 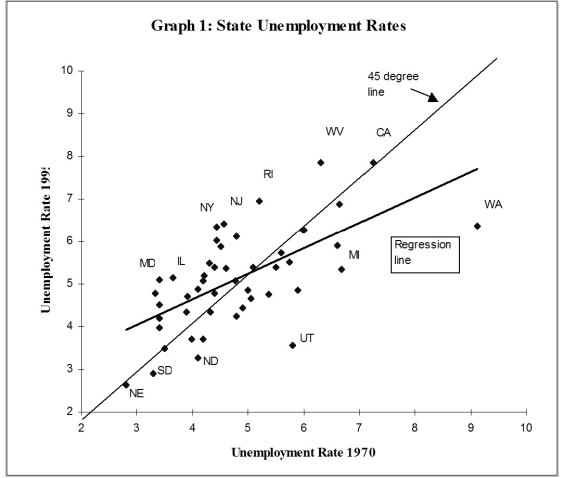 (d)One of your peers points out that this result makes little sense,since it implies that eventually all states would have identical unemployment rates.Explain the argument.
(d)One of your peers points out that this result makes little sense,since it implies that eventually all states would have identical unemployment rates.Explain the argument.
(e)Imagine that state unemployment rates were determined by their natural rates and some transitory shock.The natural rates themselves may be functions of the unemployment insurance benefits of the state,unionization rates of its labor force,demographics,sectoral composition,etc.The transitory components may include state-specific shocks to its terms of trade such as raw material movements and demand shocks from the other states.You specify the i-th state unemployment rate accordingly as follows for the two periods when you observe it, 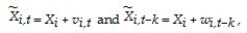 so that actual unemployment rates are measured with error.You have also assumed that the natural rate is the same for both periods.Subtracting the second period from the first then results in the following population regression function:
so that actual unemployment rates are measured with error.You have also assumed that the natural rate is the same for both periods.Subtracting the second period from the first then results in the following population regression function: 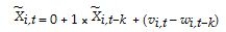 It is not too hard to show that estimation of the observed unemployment rate in period t on the unemployment rate in period (t-k)by OLS results in an estimator for the slope coefficient that is biased towards zero.The formula is
It is not too hard to show that estimation of the observed unemployment rate in period t on the unemployment rate in period (t-k)by OLS results in an estimator for the slope coefficient that is biased towards zero.The formula is  .
.
Using this insight,explain over which periods you would expect the slope to be closer to one,and over which period it should be closer to zero.
(f)Estimating the same regression for a different time period results in 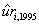 = 3.19 + 0.27 ×
= 3.19 + 0.27 ×  ;R2 = 0.21,SER = 1.03
;R2 = 0.21,SER = 1.03
(0.56)(0.07)
If your above analysis is correct,what are the implications for this time period?
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q22: Possible solutions to omitted variable bias, when
Q24: Threats to in internal validity lead to
A)perfect
Q26: In the case of errors-in-variables bias,the precise
Q27: You have decided to analyze the year-to-year
Q28: Your textbook used the California Standardized Testing
Q29: The Phillips curve is a relationship in
Q30: The true causal effect might not be
Q32: A statistical analysis is internally valid if
A)all
Q33: Keynes postulated that the marginal propensity to
Q34: Sir Francis Galton (1822-1911),an anthropologist and cousin
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents