At the Stock and Watson (http://www.pearsonhighered.com/stock_watson)website go to Student Resources and select the option "Datasets for Replicating Empirical Results." Then select the "California Test Score Data Used in Chapters 4-9" (caschool.xls)and open it in a spreadsheet program such as Excel.
In this exercise you will estimate various statistics of the Linear Regression Model with One Regressor through construction of various sums and ratio within a spreadsheet program.
Throughout this exercise,let Y correspond to Test Scores (testscore)and X to the Student Teacher Ratio (str).To generate answers to all exercises here,you will have to create seven columns and the sums of five of these.They are
(i)Yi, (ii)Xi, (iii)(Yi-  ), (iv)(Xi-
), (iv)(Xi- 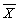 ), (v)(Yi-
), (v)(Yi- 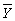 )×(Xi-
)×(Xi- 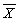 ), (vi)(Xi-
), (vi)(Xi- 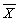 )2, (vii)(Yi-
)2, (vii)(Yi- 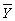 )2
)2
Although neither the sum of (iii)or (iv)will be required for further calculations,you may want to generate these as a check (both have to sum to zero).
a.Use equation (4.7)and the sums of columns (v)and (vi)to generate the slope of the regression.
b.Use equation (4.8)to generate the intercept.
c.Display the regression line (4.9)and interpret the coefficients.
d.Use equation (4.16)and the sum of column (vii)to calculate the regression R2.
e.Use equation (4.19)to calculate the SER.
f.Use the "Regression" function in Excel to verify the results.
Correct Answer:
Verified
Column (ii): 19.6...
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q48: In order to calculate the regression R2
Q49: Indicate in a scatterplot what the data
Q50: Prove that the regression R2 is identical
Q51: (Requires Appendix material)Show that the two alternative
Q52: Imagine that you had discovered a relationship
Q54: The help function for a commonly used
Q55: (Requires Calculus)Consider the following model:
Yi = β0
Q56: Show first that the regression R2 is
Q57: (Requires Appendix material)A necessary and sufficient condition
Q58: In order to calculate the slope,the intercept,and
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents