Assume that two presidential candidates,call them Bush and Gore,receive 50% of the votes in the population.You can model this situation as a Bernoulli trial,where Y is a random variable with success probability Pr(Y = 1)= p,and where Y = 1 if a person votes for Bush and Y = 0 otherwise.Furthermore,let 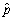 be the fraction of successes (1s)in a sample,which is distributed N(p,
be the fraction of successes (1s)in a sample,which is distributed N(p, 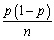 )in reasonably large samples,say for n ≥ 40.
)in reasonably large samples,say for n ≥ 40.
(a)Given your knowledge about the population,find the probability that in a random sample of 40,Bush would receive a share of 40% or less.
(b)How would this situation change with a random sample of 100?
(c)Given your answers in (a)and (b),would you be comfortable to predict what the voting intentions for the entire population are if you did not know p but had polled 10,000 individuals at random and calculated 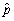 ? Explain.
? Explain.
(d)This result seems to hold whether you poll 10,000 people at random in the Netherlands or the United States,where the former has a population of less than 20 million people,while the United States is 15 times as populous.Why does the population size not come into play?
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q20: With i.i.d.sampling each of the following is
Q21: Degrees of freedom
A)in the context of the
Q22: When testing for differences of means,the t-statistic
Q23: The standard error for the difference in
Q24: When testing for differences of means,you can
Q26: Assume that you have 125 observations on
Q27: When the sample size n is large,the
Q28: You have collected data on the average
Q29: Math SAT scores (Y)are normally distributed with
Q30: The sample covariance can be calculated in
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents