Assume that Y is normally distributed N(μ,σ2) .To find Pr(c1 ≤ Y ≤ c2) ,where c1 < c2 and di = 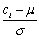 ,you need to calculate Pr(d1 ≤ Z ≤ d2) =
,you need to calculate Pr(d1 ≤ Z ≤ d2) =
A) Φ(d2) - Φ(d1)
B) Φ(1.96) - Φ(1.96)
C) Φ(d2) - (1 - Φ(d1) )
D) 1 - (Φ(d2) - Φ(d1) )
Correct Answer:
Verified
Q6: The cumulative probability distribution shows the probability
A)that
Q8: The correlation between X and Y
A)cannot be
Q9: The conditional distribution of Y given X
Q11: If variables with a multivariate normal distribution
Q11: The expected value of a discrete random
Q12: Let Y be a random variable.Then var(Y)equals
A)
Q15: The conditional expectation of Y given X,E(Y
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents