(Requires Appendix material)If the Gauss-Markov conditions hold,then OLS is BLUE.In addition,assume here that X is nonrandom.Your textbook proves the Gauss-Markov theorem by using the simple regression model Yi = β0 + β1Xi + ui and assuming a linear estimator 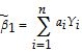 .Substitution of the simple regression model into this expression then results in two conditions for the unbiasedness of the estimator:
.Substitution of the simple regression model into this expression then results in two conditions for the unbiasedness of the estimator: 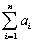 = 0 and
= 0 and 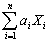 = 1.
= 1.
The variance of the estimator is var( 
 X1,…,Xn)=
X1,…,Xn)= 
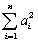 .
.
Different from your textbook,use the Lagrangian method to minimize the variance subject to the two constraints.Show that the resulting weights correspond to the OLS weights.
Correct Answer:
Verified
L =
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q39: The large-sample distribution of Q40: Assume that var(ui|Xi)= θ0+θ1 Q41: Consider estimating a consumption function from a Q42: Consider the model Yi - β1Xi + Q44: Consider the simple regression model Yi = Q46: (Requires Appendix material)Your textbook considers various distributions Q47: Your textbook states that an implication of Q48: (Requires Appendix material)This question requires you to Q49: (Requires Appendix material)State and prove the Cauchy-Schwarz Q49: For this question you may assume that![]()
![]()
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents