A study analyzed the probability of Major League Baseball (MLB)players to "survive" for another season,or,in other words,to play one more season.The researchers had a sample of 4,728 hitters and 3,803 pitchers for the years 1901-1999.All explanatory variables are standardized.The probit estimation yielded the results as shown in the table:
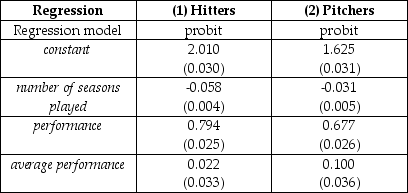 where the limited dependent variable takes on a value of one if the player had one more season (a minimum of 50 at bats or 25 innings pitched),number of seasons played is measured in years,performance is the batting average for hitters and the earned run average for pitchers,and average performance refers to performance over the career.
where the limited dependent variable takes on a value of one if the player had one more season (a minimum of 50 at bats or 25 innings pitched),number of seasons played is measured in years,performance is the batting average for hitters and the earned run average for pitchers,and average performance refers to performance over the career.
(a)Interpret the two probit equations and calculate survival probabilities for hitters and pitchers at the sample mean.Why are these so high?
(b)Calculate the change in the survival probability for a player who has a very bad year by performing two standard deviations below the average (assume also that this player has been in the majors for many years so that his average performance is hardly affected).How does this change the survival probability when compared to the answer in (a)?
(c)Since the results seem similar,the researcher could consider combining the two samples.Explain in some detail how this could be done and how you could test the hypothesis that the coefficients are the same.
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q20: In the expression Pr(Y = 1
Q22: Consider the following logit regression:
Pr(Y = 1
Q23: (Requires Advanced material)Nonlinear least squares estimators in
Q23: A study investigated the impact of house
Q26: The following problems could be analyzed using
Q26: When estimating probit and logit models,
A)the t-statistic
Q27: A study tried to find the determinants
Q28: To measure the fit of the probit
Q30: Probit coefficients are typically estimated using
A)the OLS
Q30: In the probit regression,the coefficient β1 indicates
A)the
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents