The Poisson distribution is a discrete distribution that expresses the probability of a fixed number of events occurring in a fixed interval.For example,suppose we want to model the number of arrivals per minute at the campus dining hall during lunch.We observe the actual arrivals in 200 one-minute periods in 1 week.The sample mean is 3.8 and the results are shown below.  The probabilities based on a Poisson distribution with a mean of 3.8 are shown below.
The probabilities based on a Poisson distribution with a mean of 3.8 are shown below. 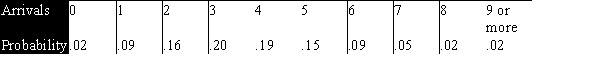 Perform a formal test to determine if the observed counts are compatible with the Poisson distribution with a mean of 3.8 and a significance level of .05.
Perform a formal test to determine if the observed counts are compatible with the Poisson distribution with a mean of 3.8 and a significance level of .05.
A) The P-value is very small;therefore the observed counts are compatible with the Poisson distribution.
B) The P-value is large;therefore the observed counts are compatible with the Poisson distribution.
C) The P-value is very small;therefore the observed counts are not compatible with the Poisson distribution.
D) The P-value is large;therefore the observed counts are not compatible with the Poisson distribution.
Correct Answer:
Verified
Q65: Because statistical software plays such an important
Q66: The null hypothesis for the chi-square test
Q67: A study was performed to examine the
Q68: How are expected cell counts computed in
Q69: When computing the column portions for a
Q71: Which of the following could be
Q72: Because statistical software plays such an important
Q73: A study was performed to examine the
Q74: Because statistical software plays such an important
Q75: The Poisson distribution is a discrete distribution
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents