Exhibit: Consumption, Income, and Wealth Over the Life Cycle 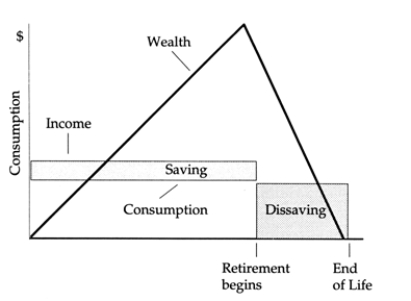 Consider the stylized pattern of lifetime income, consumption, saving, dissaving, and wealth shown in the above graph. Assume that consumption is constant over the entire lifetime, income is constant over the working lifetime, the real interest rate is zero, and there is no uncertainty about life span so that wealth equals zero at the end of life.
Consider the stylized pattern of lifetime income, consumption, saving, dissaving, and wealth shown in the above graph. Assume that consumption is constant over the entire lifetime, income is constant over the working lifetime, the real interest rate is zero, and there is no uncertainty about life span so that wealth equals zero at the end of life.
a. If there is no populati on growth, the ratio of wealth to income will be constant for the nation. If all individuals live years and work years, the amount of wealth accumulated at the time of retirement must be enough for years of consumption ( per year). What is the formula for the ratio of average wealth over the whole life cycle to consumption per year, as a function of and ? That is, what is expressed in terms of and ?
b. If and , what is the numerical value of ?
Correct Answer:
Verified
Q83: If consumers want consumption to be as
Q84: Recent research by Laibson and other economists
Q85: If a consumer is a borrower in
Q86: Recent work on the consumption function suggests
Q87: Economic data suggest that when income is
Q89: A consumer spending excessively today, intending to
Q90: Assume that Andrew Marcus is 25
Q91: Consumers with time-inconsistent preferences:
A) base consumption decisions
Q92: The life-cycle hypothesis and the permanent-income hypothesis
Q93: Whether workers must "opt into" or "opt
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents