Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If a₁, a₂, a₃, ... , an and b₁, b₂, b₃, ... , bn are geometric progressions, then a₁ b₁, a₂ b₂, a₃ b₃, ... , an bn is also a geometric progression. A) It is false. If A₁, a₂, a₃, a₄, ... = 1, 3, 6, 9,.. B₁, b₂, b₃, b₄, ... = 2, 4, 8, 16,.. Are geometric progressions, then we can see that A₁ b₁, a₂ b₂, a₃ b₃, ... = 2, 12, 48, ... Is not a geometric progression. B) It is true. A geometric progression is completely determined if the first term and the common ratio are known. Thus, if A₁, a₂, a₃, ... , a_n , ... Is a geometric progression with the first term given by a and common ratio given by r, then by definition, A₁ = a A₂ = a₁ r = ar A₃ = a₂r = ar² ^. ^. ^. An = an_-1 = ar ^{n -} ¹ Thus, we see that the product of two nths terms of two geometric progressions is given by A _nb _n = a r ⁿ ^{- 1} b 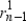where a,b are the first terms of these progressions and r, r₁ are their common ratios respectively. Then we obtain that A₁, b₁, a₂, b₂, a₃, b₃, ... , an, bn is also geometric progression with first term ab and common ratio rr₁.

Question

Quizplus · Accepted Answer

The product of two nths terms of two geometric progressions is given by A_nb_n=arⁿ^-1b11eab448_e810_79a0_acdb_cf339ff39e10_TB6027_11 where a,b are the first terms of these progressions and r, r₁ are their common ratios respectively. Using this formula, we can see that the product of the nth terms of two geometric progressions is also a geometric progression with first term ab and common ratio rr₁.

Determine Whether the Statement Is True or False