Here are data about the average January low temperature in cities in the United States, and factors that might allow us to
predict temperature. The data, available for 55 cities, include:  We will attempt to make a regression model to help account for mean January temperature and to understand the effects of
We will attempt to make a regression model to help account for mean January temperature and to understand the effects of
the various predictors.
At each step of the analysis you may assume that things learned earlier in the process are known.
Units Note: The "degrees" of temperature, given here on the Fahrenheit scale, have only coincidental language relationship to
the "degrees" of longitude and latitude. The geographic "degrees" are based on modeling the Earth as a sphere and dividing it
up into 360 degrees for a full circle. Thus 180 degrees of longitude is halfway around the world from Greenwich, England
(0°) and Latitude increases from 0 degrees at the Equator to 90 degrees of (North) latitude at the North Pole. 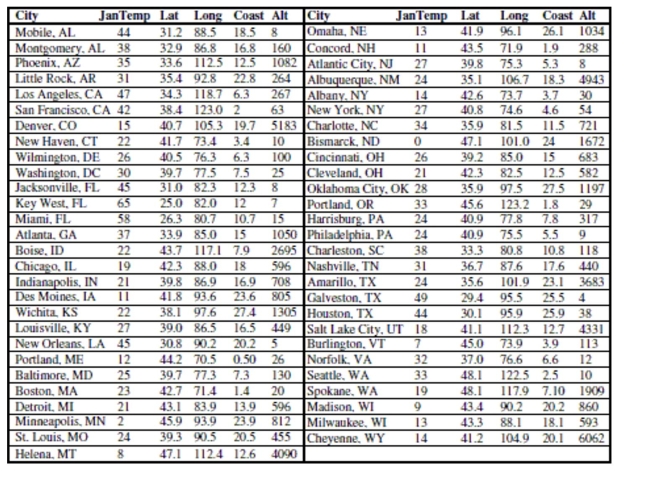
-It is possible that the distance that a city is from the ocean could affect its average January
low temperature. Coast gives an approximate distance of each city from the East Coast or
West Coast (whichever is nearer). Including it in the regression yields the following
regression table: Dependent variable is:JanTemp
R squared squared (adjusted) with degrees of freedom
And here is a scatterplot of the residuals: 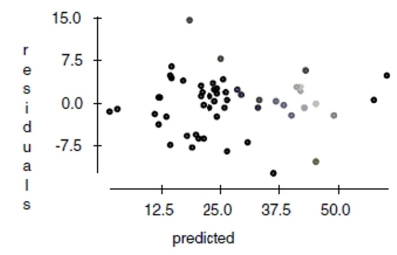
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q1: In ANOVA, an interaction between two factors
Q2: Homelessness is a problem in many
Q3: In regression an observation has high leverage
Q4: Check the conditions for the regression and
Q5: Engineers want to know what factors
Q7: In ANOVA, the Bonferroni method is used
Q8: To discourage cheating, a professor makes
Q10: Which of the following are NOT
Q11: The problem of collinearity occurs when
A) at
Q32: Of the 23 first year male
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents