Which of the following are solutions to the homogeneous second-order differential equation 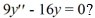 ?
?
Select all that apply.
A) , where is any real constant
B)
C) , where is any real constant
D) , where is any real constant
E)
F)
Correct Answer:
Verified
Q1: What is the characteristic equation for the
Q2: For which of these differential equations is
Q3: For which of these differential equations is
Q4: For which of these differential equations is
Q5: Which of the following are solutions
Q7: Which of the following is the
Q8: Which of the following is the
Q9: For which of the following values
Q10: What is the solution of the
Q11: Consider the second-order homogeneous differential equation
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents