(See Problem 11.) Jonas's expected utility function is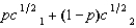 
, where p is the probability that he consumes c1 and 1 - p is the probability that he consumes c2. Jonas is offered a choice between getting a sure payment of $Z or a lottery in which he receives $3,600 with probability .10 or $6,400 with probability .90. Jonas will choose the sure payment if
A) Z > 6,084 and the lottery if Z < 6,084.
B) Z > 4,842 and the lottery if Z < 4,842.
C) Z > 6,400 and the lottery if Z < 6,400.
D) Z > 6,242 and the lottery if Z < 6,242.
E) Z > 6,120 and the lottery if Z < 6,120.
Correct Answer:
Verified
Q1: (See Problem 2.) Willy's only source of
Q2: In Problem 9, Billy has a von
Q4: (See Problem 11.) Pete's expected utility function
Q5: In Problem 9, Billy has a von
Q6: In Problem 9, Billy has a von
Q7: (See Problem 11.) Lawrence's expected utility function
Q8: Sally Kink is an expected utility maximizer
Q9: (See Problem 11.) Albert's expected utility function
Q10: Sally Kink is an expected utility maximizer
Q11: (See Problem 2.) Willy's only source of
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions
Scan the QR code to install the App and get 2 free unlocks
Unlock quizzes for free by uploading documents