Multiple Choice
The 2-manifold M in R4 given by the equations 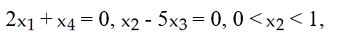 0 < x4 < 1,
0 < x4 < 1,
0 < < 1 has normals 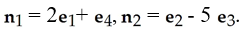 It is oriented by the 2-form
It is oriented by the 2-form
ω(x) ( v1 , v2 ) = det( n1 n2 v1 v2 ) . Let be a parametrization for M. Which of the following statements is true?
A) P is orientation preserving for M.
B) P does not determine an orientation for M.
C) P is orientation reversing for M, but no orientation preserving parametrization for M exists.
D) P is orientation reversing for M, but q(u) = ( 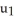 , 5
, 5 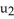 ,
, 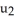 , -2
, -2 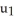 ) would be orientation preserving parametrization for M.
) would be orientation preserving parametrization for M.
E) P is orientation reversing for M, but q(u) = (- 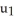 , 5
, 5 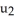 ,
, 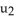 , 2
, 2  ) would be an orientation-preserving parametrization for M.
) would be an orientation-preserving parametrization for M.
Correct Answer:
Verified
Related Questions
Q57: One way to describe a smooth k-manifold


