Let M be the smooth 2-manifold 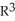 , x = p( ,
, x = p( ,  ) = (cos( )sin(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ), sin( )sin(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ), cos(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ),0 2 , and let 11ee77e1_7793_40f8_a0f8_f10db821b3f0_TB9661_11 be a parametrization for M. If M is oriented by the differential 2-form 11ee7bce_4c5c_2301_ae82_cd6516243ba0_TB9661_11 = zdx11ee7bce_59c0_5432_ae82_19d52c3b82fe_TB9661_11 dy, determine whether the parametrization p is orientation preserving or orientation reversing for M.
) = (cos( )sin(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ), sin( )sin(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ), cos(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ),0 2 , and let 11ee77e1_7793_40f8_a0f8_f10db821b3f0_TB9661_11 be a parametrization for M. If M is oriented by the differential 2-form 11ee7bce_4c5c_2301_ae82_cd6516243ba0_TB9661_11 = zdx11ee7bce_59c0_5432_ae82_19d52c3b82fe_TB9661_11 dy, determine whether the parametrization p is orientation preserving or orientation reversing for M.
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q61: Calculate Q62: The 2-manifold M in R4 given Q63: Find Q64: Evaluate the integral of Q65: If M is the part of the Q67: Consider the unit cube Q = Q68: Let S be a piece with boundary Q69: Use the generalized Stokes's Theorem to find Q70: Use the generalized Stokes's Theorem to Q71: Integrate the differential 3-form Unlock this Answer For Free Now! View this answer and more for free by performing one of the following actions Scan the QR code to install the App and get 2 free unlocks Unlock quizzes for free by uploading documents![]()
![]()

![]()

