Solved

According to a Study Conducted in One City, 34% of Adults

Question 12

Multiple Choice

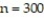According to a study conducted in one city, 34% of adults in the city have credit card debts of more than $2000. A simple random sample of According to a study conducted in one city, 34% of adults in the city have credit card debts of more than $2000. A simple random sample of adults is obtained from the city. Describe the sampling distribution of , the sample proportion of adults who have credit card debts of more than $2000. A) Exactly normal; = 0.34, = 0.027 B) Approximately normal; = 0.34, = 0.0007 C) Binomial; = 102, = 8.20 D) Approximately normal; = 0.34, = 0.027 adults is obtained from the city. 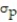Describe the sampling distribution of According to a study conducted in one city, 34% of adults in the city have credit card debts of more than $2000. A simple random sample of adults is obtained from the city. Describe the sampling distribution of , the sample proportion of adults who have credit card debts of more than $2000. A) Exactly normal; = 0.34, = 0.027 B) Approximately normal; = 0.34, = 0.0007 C) Binomial; = 102, = 8.20 D) Approximately normal; = 0.34, = 0.027 , the sample proportion of adults who have credit card debts of more than $2000.


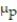A) Exactly normal; According to a study conducted in one city, 34% of adults in the city have credit card debts of more than $2000. A simple random sample of adults is obtained from the city. Describe the sampling distribution of , the sample proportion of adults who have credit card debts of more than $2000. A) Exactly normal; = 0.34, = 0.027 B) Approximately normal; = 0.34, = 0.0007 C) Binomial; = 102, = 8.20 D) Approximately normal; = 0.34, = 0.027 = 0.34, According to a study conducted in one city, 34% of adults in the city have credit card debts of more than $2000. A simple random sample of adults is obtained from the city. Describe the sampling distribution of , the sample proportion of adults who have credit card debts of more than $2000. A) Exactly normal; = 0.34, = 0.027 B) Approximately normal; = 0.34, = 0.0007 C) Binomial; = 102, = 8.20 D) Approximately normal; = 0.34, = 0.027 = 0.027
B) Approximately normal; According to a study conducted in one city, 34% of adults in the city have credit card debts of more than $2000. A simple random sample of adults is obtained from the city. Describe the sampling distribution of , the sample proportion of adults who have credit card debts of more than $2000. A) Exactly normal; = 0.34, = 0.027 B) Approximately normal; = 0.34, = 0.0007 C) Binomial; = 102, = 8.20 D) Approximately normal; = 0.34, = 0.027 = 0.34, According to a study conducted in one city, 34% of adults in the city have credit card debts of more than $2000. A simple random sample of adults is obtained from the city. Describe the sampling distribution of , the sample proportion of adults who have credit card debts of more than $2000. A) Exactly normal; = 0.34, = 0.027 B) Approximately normal; = 0.34, = 0.0007 C) Binomial; = 102, = 8.20 D) Approximately normal; = 0.34, = 0.027 = 0.0007
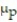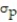C) Binomial; According to a study conducted in one city, 34% of adults in the city have credit card debts of more than $2000. A simple random sample of adults is obtained from the city. Describe the sampling distribution of , the sample proportion of adults who have credit card debts of more than $2000. 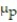A) Exactly normal; = 0.34, = 0.027 B) Approximately normal; = 0.34, = 0.0007 C) Binomial; = 102, = 8.20 D) Approximately normal; = 0.34, = 0.027 = 102, According to a study conducted in one city, 34% of adults in the city have credit card debts of more than $2000. A simple random sample of adults is obtained from the city. Describe the sampling distribution of , the sample proportion of adults who have credit card debts of more than $2000. A) Exactly normal; = 0.34, = 0.027 B) Approximately normal; = 0.34, = 0.0007 C) Binomial; = 102, = 8.20 D) Approximately normal; = 0.34, = 0.027 = 8.20
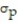D) Approximately normal; According to a study conducted in one city, 34% of adults in the city have credit card debts of more than $2000. A simple random sample of adults is obtained from the city. Describe the sampling distribution of , the sample proportion of adults who have credit card debts of more than $2000. A) Exactly normal; = 0.34, = 0.027 B) Approximately normal; = 0.34, = 0.0007 C) Binomial; = 102, = 8.20 D) Approximately normal; = 0.34, = 0.027 = 0.34, According to a study conducted in one city, 34% of adults in the city have credit card debts of more than $2000. A simple random sample of adults is obtained from the city. Describe the sampling distribution of , the sample proportion of adults who have credit card debts of more than $2000. A) Exactly normal; = 0.34, = 0.027 B) Approximately normal; = 0.34, = 0.0007 C) Binomial; = 102, = 8.20 D) Approximately normal; = 0.34, = 0.027 = 0.027

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q2: Determine Determine and</p></div><svg width=

Q3: What are the values of

Q4: What are the values of

Q5: The standard error of the mean is

Q6: The amount of money collected by a

Q7: A farmer was interested in determining how

Q8: A farmer was interest in determining how

Q9: A farmer was interested in determining how

Q10: Describe the sampling distribution of

Q11: A simple random sample of size n

Unlock this Answer For Free Now!

View this answer and more for free by performing one of the following actions

qr-code

Scan the QR code to install the App and get 2 free unlocks

upload documents

Unlock quizzes for free by uploading documents