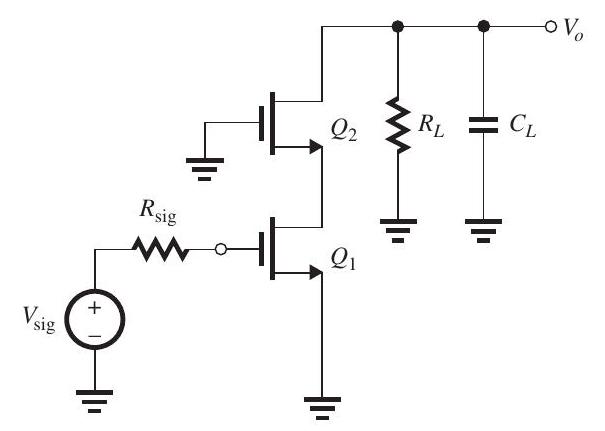
Figure 105 $g_{m}=2 \mathrm{~mA} / \mathrm{V}$ And $r_{o}=20 \mathrm{k} \Omega$ And Has $R_{\text {sig }}=R_{L}=20 \mathrm{k} \Omega$

Figure 10.5.1


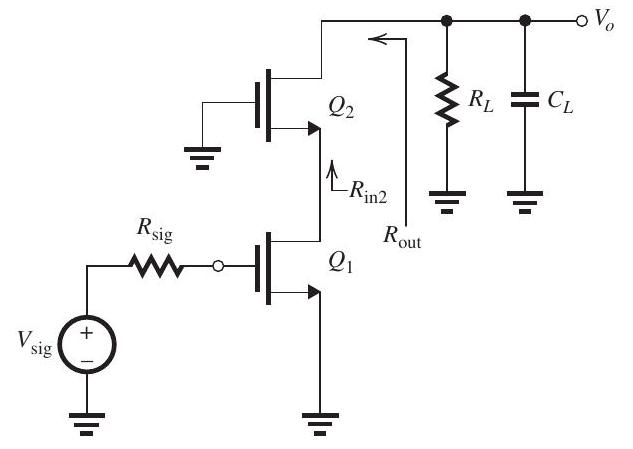
Figure 10.5.2
(a) The MOSFET in the common-source amplifier in Fig. 10.5.1, where the dc bias arrangement is not shown, is operating at $g_{m}=2 \mathrm{~mA} / \mathrm{V}$ and $r_{o}=20 \mathrm{k} \Omega$ and has $R_{\text {sig }}=R_{L}=20 \mathrm{k} \Omega$ . The transistor capacitances are specified as $C_{g s}=40 \mathrm{fF}$ and $C_{g d}=C_{d b}=10 \mathrm{fF}$ . Also, there is an additional capacitance between the output node and ground, $C_{L}=10 \mathrm{fF}$ . Find the overall de gain $G_{v} \equiv V_{o} / V_{\text {sig }}$ , the upper 3-dB frequency $f_{H}$ , and the gain-bandwidth product $f_{t}$ . To determine $f_{H}$ , use the method of open-circuit time constants and recall that the resistance seen by $C_{g d}$ is given by $R_{g d}=\left(1+g_{m} R_{L}^{\prime}\right) R_{\text {sig }}+R_{L}^{\prime}$ , where $R_{L}^{\prime}=R_{L} \| r_{o}$ .
(b) To increase $f_{t}$ , the common-source transistor $Q_{1}$ is cascoded as shown in Fig. 10.5.2 (refer to Figure above), where the dc bias arrangement is not shown. For the same values of $R_{\mathrm{sig}}, R_{L}$ , and $C_{L}$ as in (a), assuming $Q_{1}$ and $Q_{2}$ are biased so that $g_{m 1}=g_{m 2}=2 \mathrm{~mA} / \mathrm{V}$ and $r_{o 1}=r_{o 2}=20 \mathrm{k} \Omega$ , and for the capacitances of $Q_{1}$ and $Q_{2}$ to have the same values as specified in (a) above, find $G_{v}, f_{H}$ , and $f_{t}$ for the cascode amplifier. Recall that $R_{\text {out }} \simeq\left(g_{m} r_{o}\right) r_{o}$ and $R_{\text {in } 2}=\frac{1}{g_{m 2}}+\frac{R_{L}}{g_{m 2} r_{o 2}}$ .
In using the open-circuit time-constants method, adapt the formula given in (a) for $R_{g d}$ to obtain $R_{g d 1}$ . By what factor is $f_{t}$ increased?