The Amplifier in Fig $R_{\text {sig }}=1 \mathrm{k} \Omega, C_{B}=1 \mu \mathrm{F}, C_{E}=10$

The amplifier in Fig. 10.7.1


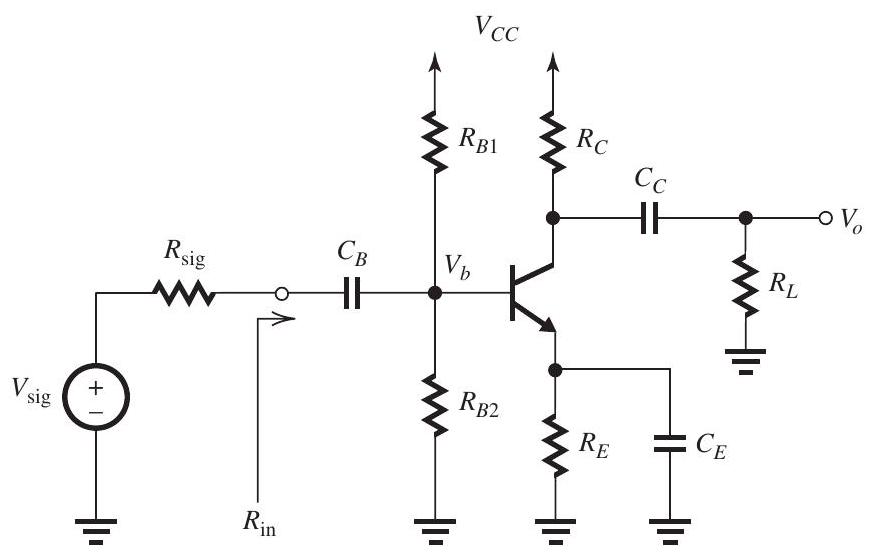
Figure 10.7.1
has $R_{\text {sig }}=1 \mathrm{k} \Omega, C_{B}=1 \mu \mathrm{F}, C_{E}=10$ $\mu \mathrm{F}, C_{C}=1 \mu \mathrm{F}, R_{L}=8 \mathrm{k} \Omega, V_{B E}=0.7 \mathrm{~V}$ , and $V_{C C}=15 \mathrm{~V}$ .
(a) Assuming $\beta=\infty$ , find $R_{B 1}, R_{B 2}, R_{E}$ , and $R_{C}$ to operate the BJT at a dc bias point characterized by $I_{C}=1 \mathrm{~mA}$ and $V_{C}=7 \mathrm{~V}$ . Design for $V_{B}=5 \mathrm{~V}$ and a voltage-divider current of $0.1 \mathrm{~mA}$ .
(b) Find $r_{e}, g_{m}$ , and $r_{\pi}$ , assuming $\beta=100$ .
(c) At midband frequencies, find $R_{\text {in }}, V_{b} / V_{\text {sig }}$ , $V_{o} / V_{b}$ , and $V_{o} / V_{\text {sig }}$ , assuming $\beta=100$ .
(d) In the low-frequency band use the method of short-circuit time constants to obtain an estimate of the 3-dB frequency, $f_{L}$ .
(e) If $C_{\pi}=10 \mathrm{pF}$ and $C_{\mu}=1 \mathrm{pF}$ , use the Miller approximation to determine the input capacitance of the amplifier at high frequencies, and hence determine an estimate of the high-frequency $3 \mathrm{~dB}$ frequency, $f_{H}$ .