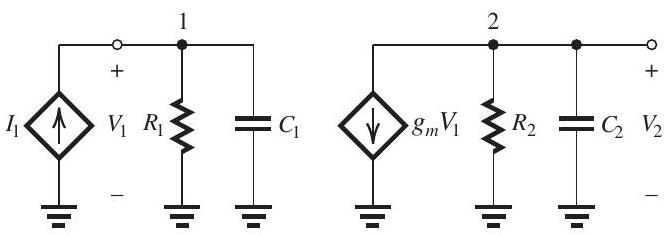
Figure 119 $100 \mathrm{~dB}$ And Three Real-Axis Poles with Frequencies $f_{P 1}=10^{4} \mathrm{~Hz}$

Figure 11.9.1
An op amp has a dc gain of $100 \mathrm{~dB}$ and three real-axis poles with frequencies $f_{P 1}=10^{4} \mathrm{~Hz}$ , $f_{P 2}=10^{5} \mathrm{~Hz}$ , and $f_{P 3}=10^{6} \mathrm{~Hz}$ . The op-amp internal circuit includes an amplifier stage having the equivalent circuit shown in Fig. 11.9.1, where $C_{1}=100 \mathrm{pF}, g_{m}=20 \mathrm{~mA} / \mathrm{V}$ , and $C_{2}=10 \mathrm{pF}$ . Furthermore, it is found that the input circuit of this stage is responsible for the pole at $f_{P 1}$ and that the output circuit is responsible for the pole at $f_{P 2}$ . It is required to frequency-compensate this op amp so that it becomes stable in closed-loop configurations with a closed-loop gain as low as unity.
(a) Sketch and clearly label a Bode plot for the op amp gain. Use a frequency axis that extends from $0.1 \mathrm{~Hz}$ to $10^{7} \mathrm{~Hz}$ .
(b) If the frequency compensation is achieved by connecting a capacitor $C_{C}$ in parallel with $C_{1}$ , find the required value of $C_{C}$ and sketch the modified gain response on your Bode plot.
(c) If the frequency compensation is achieved by placing a capacitor $C_{f}$ in the feedback path of the amplifier stage in Fig. 11.9.1 -that is, between nodes 1 and 2 (Miller compensation)-find the required value of $C_{f}$ . Also, find the new frequencies of the poles and sketch the modified gain on your Bode plot.