Consider the following parametric linear programming problem,where the parameter $\theta$ must be nonnegative: Maximize Z($\theta$)= (5 + 2$\theta$)x₁ + (2 - $\theta$)x₂ + (3 + $\theta$)x₃,subject to 4x₁ + x₂ ≥ 5 + 5$\theta$ , 3x₁ + x₂ + 2x₃ = 10 - 10$\theta$ ,x₁ ≥ 0,x₂ ≥ 0,x₃ ≥ 0.Let x₄ be the surplus variable for the first functional constraint,and let 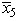and be the artificial variables for the respective functional constraints.After we apply the simplex method with the Big M method and with $\theta$ = 0,the final simplex tableau is (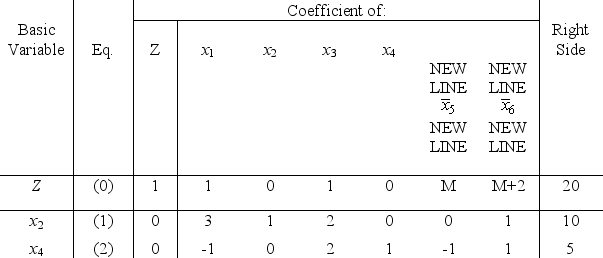a)Use the fundamental insight (Sec.5.3 in the textbook)to revise this tableau to reflect the inclusion of the parameter $\theta$ in the original model.Show the complete tableau needed to apply the feasibility test and the optimality test for any value of $\theta$.Express the corresponding basic solution (and Z)as a function of $\theta$. (b)Determine the range of nonnegative values of $\theta$ over which this basic solution is feasible. (c)Determine the range of nonnegative values of $\theta$ over which this basic solution is both feasible and optimal.Determine the best choice of $\theta$ over this range.

Question

Quizplus · Accepted Answer

The Answer is (a)To apply the fundamental insight,we need to recognize that it is the artificial variables whose coefficients in Rows 1 and 2 of the initial tableau form an identity matrix.Therefore,by the logic of the fundamental insight,it is the coefficients of these variables in the final tableau that play the same role as the coefficients of the slack variables when the original problem is in our standard form.In other words,using the notation of Sec.5.3,S* = $(a)To apply the fundamental insight,we need to recognize that it is the artificial variables whose coefficients in Rows 1 and 2 of the initial tableau form an identity matrix.Therefore,by the logic of the fundamental insight,it is the coefficients of these variables in the final tableau that play the same role as the coefficients of the slack variables when the original problem is in our standard form.In other words,using the notation of Sec.5.3,S* = .Similarly,y* = [M M+2] - [M M] = [0 2] gives the increase in the coefficients of these variables over their original values in the initial tableau before restoring proper form from Gaussian elimination.(The notation of Sec.5.2,replacing S* by B-1 and replacing y* by cBB-1,also may be used instead.)Proceeding with S* and y* in the usual way to determine the rest of the revised final tableau,the new right-hand side is S*b = .The changes in the objective function change the final Row 0 (excluding the right-hand side)to Row 0 = [1-2 heta , heta ,1- heta ,0,M,M+2] However,since x2 is a basic variable,proper form from Gaussian elimination requires that elementary row operations be used to give it a coefficient of 0.Therefore,new Row 0 = old Row 0 - heta * (Row 1)= [1-2 heta , heta ,1- heta ,0,M,M+2] - heta [3,1,2,0,0,1] = [1-5 heta ,0,1-3 heta ,0,M,M+2- heta ],so y* now becomes y* = [0 2- heta ].Finally,because of the changes in the original right-hand sides,the new right-hand side in Row 0 is y*b = [0 2- heta ] = 20 - 30 heta + 10 heta 2.The complete tableau is (b)To be feasible,we need 10 -10 heta \ge 0,5 - 15 heta \ge 0,which implies that 0 \le heta \le 1/3. (c)To be optimal,1 -5 heta \ge 0,1 - 3 heta \ge 0,which implies that 0 \le heta \le 1/5.Hence,0 \le heta \le 1/5 is needed to be feasible and optimal.So the basic solution is (x1*,x2*)= (0,10-10 heta ),with Z*( heta )= 20-30 heta +10 heta 2 for 0 \le heta \le 1/5.The best choice for heta is the one that maximizes Z*( heta )over 0 \le heta \le 1/5.Since = -30 + 20 heta < 0 for 0≤ heta ≤ 1/5,we conclude that heta = 0 is the best choice of heta over this range.$ .Similarly,y* = [M M+2] - [M M] = [0 2] gives the increase in the coefficients of these variables over their original values in the initial tableau before restoring proper form from Gaussian elimination.(The notation of Sec.5.2,replacing S* by B^-1 and replacing y* by c_BB^-1,also may be used instead.)Proceeding with S* and y* in the usual way to determine the rest of the revised final tableau,the new right-hand side is S*b = $(a)To apply the fundamental insight,we need to recognize that it is the artificial variables whose coefficients in Rows 1 and 2 of the initial tableau form an identity matrix.Therefore,by the logic of the fundamental insight,it is the coefficients of these variables in the final tableau that play the same role as the coefficients of the slack variables when the original problem is in our standard form.In other words,using the notation of Sec.5.3,S* = .Similarly,y* = [M M+2] - [M M] = [0 2] gives the increase in the coefficients of these variables over their original values in the initial tableau before restoring proper form from Gaussian elimination.(The notation of Sec.5.2,replacing S* by B-1 and replacing y* by cBB-1,also may be used instead.)Proceeding with S* and y* in the usual way to determine the rest of the revised final tableau,the new right-hand side is S*b = .The changes in the objective function change the final Row 0 (excluding the right-hand side)to Row 0 = [1-2 heta , heta ,1- heta ,0,M,M+2] However,since x2 is a basic variable,proper form from Gaussian elimination requires that elementary row operations be used to give it a coefficient of 0.Therefore,new Row 0 = old Row 0 - heta * (Row 1)= [1-2 heta , heta ,1- heta ,0,M,M+2] - heta [3,1,2,0,0,1] = [1-5 heta ,0,1-3 heta ,0,M,M+2- heta ],so y* now becomes y* = [0 2- heta ].Finally,because of the changes in the original right-hand sides,the new right-hand side in Row 0 is y*b = [0 2- heta ] = 20 - 30 heta + 10 heta 2.The complete tableau is (b)To be feasible,we need 10 -10 heta \ge 0,5 - 15 heta \ge 0,which implies that 0 \le heta \le 1/3. (c)To be optimal,1 -5 heta \ge 0,1 - 3 heta \ge 0,which implies that 0 \le heta \le 1/5.Hence,0 \le heta \le 1/5 is needed to be feasible and optimal.So the basic solution is (x1*,x2*)= (0,10-10 heta ),with Z*( heta )= 20-30 heta +10 heta 2 for 0 \le heta \le 1/5.The best choice for heta is the one that maximizes Z*( heta )over 0 \le heta \le 1/5.Since = -30 + 20 heta < 0 for 0≤ heta ≤ 1/5,we conclude that heta = 0 is the best choice of heta over this range.$ .The changes in the objective function change the final Row 0 (excluding the right-hand side)to Row 0 = [1-2

heta

,

heta

,1-

heta

,0,M,M+2] However,since x₂ is a basic variable,proper form from Gaussian elimination requires that elementary row operations be used to give it a coefficient of 0.Therefore,new Row 0 = old Row 0 -

heta

* (Row 1)= [1-2

heta

,

heta

,1-

heta

,0,M,M+2] -

heta

[3,1,2,0,0,1] = [1-5

heta

,0,1-3

heta

,0,M,M+2-

heta

],so y* now becomes y* = [0 2-

heta

].Finally,because of the changes in the original right-hand sides,the new right-hand side in Row 0 is y*b = [0 2-

heta

] $(a)To apply the fundamental insight,we need to recognize that it is the artificial variables whose coefficients in Rows 1 and 2 of the initial tableau form an identity matrix.Therefore,by the logic of the fundamental insight,it is the coefficients of these variables in the final tableau that play the same role as the coefficients of the slack variables when the original problem is in our standard form.In other words,using the notation of Sec.5.3,S* = .Similarly,y* = [M M+2] - [M M] = [0 2] gives the increase in the coefficients of these variables over their original values in the initial tableau before restoring proper form from Gaussian elimination.(The notation of Sec.5.2,replacing S* by B-1 and replacing y* by cBB-1,also may be used instead.)Proceeding with S* and y* in the usual way to determine the rest of the revised final tableau,the new right-hand side is S*b = .The changes in the objective function change the final Row 0 (excluding the right-hand side)to Row 0 = [1-2 heta , heta ,1- heta ,0,M,M+2] However,since x2 is a basic variable,proper form from Gaussian elimination requires that elementary row operations be used to give it a coefficient of 0.Therefore,new Row 0 = old Row 0 - heta * (Row 1)= [1-2 heta , heta ,1- heta ,0,M,M+2] - heta [3,1,2,0,0,1] = [1-5 heta ,0,1-3 heta ,0,M,M+2- heta ],so y* now becomes y* = [0 2- heta ].Finally,because of the changes in the original right-hand sides,the new right-hand side in Row 0 is y*b = [0 2- heta ] = 20 - 30 heta + 10 heta 2.The complete tableau is (b)To be feasible,we need 10 -10 heta \ge 0,5 - 15 heta \ge 0,which implies that 0 \le heta \le 1/3. (c)To be optimal,1 -5 heta \ge 0,1 - 3 heta \ge 0,which implies that 0 \le heta \le 1/5.Hence,0 \le heta \le 1/5 is needed to be feasible and optimal.So the basic solution is (x1*,x2*)= (0,10-10 heta ),with Z*( heta )= 20-30 heta +10 heta 2 for 0 \le heta \le 1/5.The best choice for heta is the one that maximizes Z*( heta )over 0 \le heta \le 1/5.Since = -30 + 20 heta < 0 for 0≤ heta ≤ 1/5,we conclude that heta = 0 is the best choice of heta over this range.$ = 20 - 30

heta

+ 10

heta

².The complete tableau is $(a)To apply the fundamental insight,we need to recognize that it is the artificial variables whose coefficients in Rows 1 and 2 of the initial tableau form an identity matrix.Therefore,by the logic of the fundamental insight,it is the coefficients of these variables in the final tableau that play the same role as the coefficients of the slack variables when the original problem is in our standard form.In other words,using the notation of Sec.5.3,S* = .Similarly,y* = [M M+2] - [M M] = [0 2] gives the increase in the coefficients of these variables over their original values in the initial tableau before restoring proper form from Gaussian elimination.(The notation of Sec.5.2,replacing S* by B-1 and replacing y* by cBB-1,also may be used instead.)Proceeding with S* and y* in the usual way to determine the rest of the revised final tableau,the new right-hand side is S*b = .The changes in the objective function change the final Row 0 (excluding the right-hand side)to Row 0 = [1-2 heta , heta ,1- heta ,0,M,M+2] However,since x2 is a basic variable,proper form from Gaussian elimination requires that elementary row operations be used to give it a coefficient of 0.Therefore,new Row 0 = old Row 0 - heta * (Row 1)= [1-2 heta , heta ,1- heta ,0,M,M+2] - heta [3,1,2,0,0,1] = [1-5 heta ,0,1-3 heta ,0,M,M+2- heta ],so y* now becomes y* = [0 2- heta ].Finally,because of the changes in the original right-hand sides,the new right-hand side in Row 0 is y*b = [0 2- heta ] = 20 - 30 heta + 10 heta 2.The complete tableau is (b)To be feasible,we need 10 -10 heta \ge 0,5 - 15 heta \ge 0,which implies that 0 \le heta \le 1/3. (c)To be optimal,1 -5 heta \ge 0,1 - 3 heta \ge 0,which implies that 0 \le heta \le 1/5.Hence,0 \le heta \le 1/5 is needed to be feasible and optimal.So the basic solution is (x1*,x2*)= (0,10-10 heta ),with Z*( heta )= 20-30 heta +10 heta 2 for 0 \le heta \le 1/5.The best choice for heta is the one that maximizes Z*( heta )over 0 \le heta \le 1/5.Since = -30 + 20 heta < 0 for 0≤ heta ≤ 1/5,we conclude that heta = 0 is the best choice of heta over this range.$
(b)To be feasible,we need 10 -10

heta

\ge

0,5 - 15

heta

\ge

0,which implies that 0

\le

heta

\le

1/3.
(c)To be optimal,1 -5

heta

\ge

0,1 - 3

heta

\ge

0,which implies that 0

\le

heta

\le

1/5.Hence,0

\le

heta

\le

1/5 is needed to be feasible and optimal.So the basic solution is (x₁*,x₂*)= (0,10-10

heta

),with Z*(

heta

)= 20-30

heta

+10

heta

² for 0

\le

heta

\le

1/5.The best choice for

heta

is the one that maximizes Z*(

heta

)over 0

\le

heta

\le

1/5.Since $(a)To apply the fundamental insight,we need to recognize that it is the artificial variables whose coefficients in Rows 1 and 2 of the initial tableau form an identity matrix.Therefore,by the logic of the fundamental insight,it is the coefficients of these variables in the final tableau that play the same role as the coefficients of the slack variables when the original problem is in our standard form.In other words,using the notation of Sec.5.3,S* = .Similarly,y* = [M M+2] - [M M] = [0 2] gives the increase in the coefficients of these variables over their original values in the initial tableau before restoring proper form from Gaussian elimination.(The notation of Sec.5.2,replacing S* by B-1 and replacing y* by cBB-1,also may be used instead.)Proceeding with S* and y* in the usual way to determine the rest of the revised final tableau,the new right-hand side is S*b = .The changes in the objective function change the final Row 0 (excluding the right-hand side)to Row 0 = [1-2 heta , heta ,1- heta ,0,M,M+2] However,since x2 is a basic variable,proper form from Gaussian elimination requires that elementary row operations be used to give it a coefficient of 0.Therefore,new Row 0 = old Row 0 - heta * (Row 1)= [1-2 heta , heta ,1- heta ,0,M,M+2] - heta [3,1,2,0,0,1] = [1-5 heta ,0,1-3 heta ,0,M,M+2- heta ],so y* now becomes y* = [0 2- heta ].Finally,because of the changes in the original right-hand sides,the new right-hand side in Row 0 is y*b = [0 2- heta ] = 20 - 30 heta + 10 heta 2.The complete tableau is (b)To be feasible,we need 10 -10 heta \ge 0,5 - 15 heta \ge 0,which implies that 0 \le heta \le 1/3. (c)To be optimal,1 -5 heta \ge 0,1 - 3 heta \ge 0,which implies that 0 \le heta \le 1/5.Hence,0 \le heta \le 1/5 is needed to be feasible and optimal.So the basic solution is (x1*,x2*)= (0,10-10 heta ),with Z*( heta )= 20-30 heta +10 heta 2 for 0 \le heta \le 1/5.The best choice for heta is the one that maximizes Z*( heta )over 0 \le heta \le 1/5.Since = -30 + 20 heta < 0 for 0≤ heta ≤ 1/5,we conclude that heta = 0 is the best choice of heta over this range.$ = -30 + 20

heta

< 0 for 0≤

heta

≤ 1/5,we conclude that

heta

= 0 is the best choice of

heta

over this range.

Consider the Following Parametric Linear Programming Problem,where the Parameter θ\thetaθ Must Be Nonnegative: Maximize Z

Consider the Following Parametric Linear Programming Problem,where the Parameter $\theta$ Must Be Nonnegative: Maximize Z