The random variable X has the cumulative distribution function F(x)whose value or derivative is shown below for various values of x.F(0)= 0, = ,for 0

Question

The random variable X has the cumulative distribution function F(x)whose value or derivative  is shown below for various values of x.F(0)= 0, 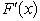 =  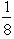,for 0 < x < 2,P(X = 2)=  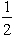,so F(2)=  ,  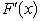=  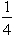,for 2 < x < 3,F(3)= 1.Generate four random observations from this probability distribution by using the following uniform random numbers:  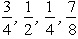.Also calculate the sample average and compare it with the true mean  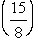for this probability distribution.

Quizplus · Accepted Answer

The Answer is

Applying the inverse transformation method,we use a uniform random number r between 0 and 1,set F(x)= r and solve for x,which then is the desired random observation.For 0 ≤ x < 2,setting

yields x = 8r for

.Because

,we have x = 2 for

.For 2 < x ≤ 3,setting

yields x = 4r - 1 for

.To summarize,the random observation x generated by the uniform random number r is

Hence,when

,we have

with average = 33/16,which is slightly above the mean of 15/8.

The Random Variable X Has the Cumulative Distribution Function F(x)whose