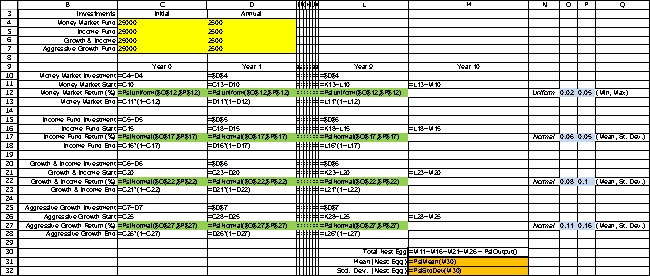
Patrick Gordon is ten years away from retirement.He has accumulated a $100,000 nest egg that he would like to invest for his golden years.Furthermore,he is confident that he can invest $10,000 more each year until retirement.He is curious about what kind of nest egg he can expect to have accumulated at retirement ten years from now.Patrick plans to split his investments evenly among four investments: a Money Market Fund,a Domestic Stock Fund,a Global Stock Fund,and an Aggressive Growth Fund.Based on past performance,Patrick expects each of these funds to earn a return in each of the upcoming ten years according to the distributions shown in the following table.  Assume that the initial nest egg ($100,000)and the first year's investment ($10,000)are made right now (year 0)and are split evenly among the four funds (i.e.,$27,500 in each fun d)in the same fund and no redistribution will be done before retirement.Furthermore,nine additional investments of $10,000 will be made and split evenly among the four funds ($2,500 each)at year 1,year 2,...,year 9.A financial advisor has told Patrick that he can retire comfortably if he can accumulate $300,000 by year 10 to supplement his other sources of retirement income.Use a 1000-trial ASPE simulation to estimate each of the following.The uncertain elements in this problem are the annual return of each investment over the next 10 years (Year 0 through Year 9).To simulate this,we define an uncertain variable cell for the annual return of each investment in each year.These cells are defined in rows 12,17,22,and 27 of the spreadsheet below.To track the investments,we calculate their balances in each year.Row 10,15,20,and 25 show the investment made by Patrick in each year.Rows 11,16,21,and 26 calculate the balance in each fund at the start of the year.For Year 0 in each fund,this will simply be the initial investment ($25,000)plus the annual investment ($2,500).For each future year,it will be the balance at the end of the preceding year plus the annual investment.For example,for Year 1 of the money market fund,the starting balance is D11 = C13 + D10.Rows 13,18,23,and 28 calculate the year-end balance for each fund.This will be the starting balance times the net return.For example,for the money market fund in Year 0 this will be C13 = C11*(1+C12).Finally,the Year 10 totals are added up in M30 to calculate Patrick's final nest egg.This cell is defined as a results cell in ASPE.Two statistic cells are defined in M31 and M32 to estimate the mean and standard deviation of the final nest egg.
Assume that the initial nest egg ($100,000)and the first year's investment ($10,000)are made right now (year 0)and are split evenly among the four funds (i.e.,$27,500 in each fun d)in the same fund and no redistribution will be done before retirement.Furthermore,nine additional investments of $10,000 will be made and split evenly among the four funds ($2,500 each)at year 1,year 2,...,year 9.A financial advisor has told Patrick that he can retire comfortably if he can accumulate $300,000 by year 10 to supplement his other sources of retirement income.Use a 1000-trial ASPE simulation to estimate each of the following.The uncertain elements in this problem are the annual return of each investment over the next 10 years (Year 0 through Year 9).To simulate this,we define an uncertain variable cell for the annual return of each investment in each year.These cells are defined in rows 12,17,22,and 27 of the spreadsheet below.To track the investments,we calculate their balances in each year.Row 10,15,20,and 25 show the investment made by Patrick in each year.Rows 11,16,21,and 26 calculate the balance in each fund at the start of the year.For Year 0 in each fund,this will simply be the initial investment ($25,000)plus the annual investment ($2,500).For each future year,it will be the balance at the end of the preceding year plus the annual investment.For example,for Year 1 of the money market fund,the starting balance is D11 = C13 + D10.Rows 13,18,23,and 28 calculate the year-end balance for each fund.This will be the starting balance times the net return.For example,for the money market fund in Year 0 this will be C13 = C11*(1+C12).Finally,the Year 10 totals are added up in M30 to calculate Patrick's final nest egg.This cell is defined as a results cell in ASPE.Two statistic cells are defined in M31 and M32 to estimate the mean and standard deviation of the final nest egg. 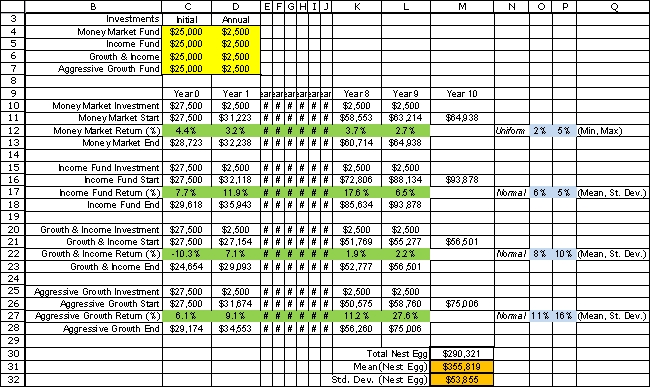
 The results of a 1000-trial simulation run are shown below.
The results of a 1000-trial simulation run are shown below. 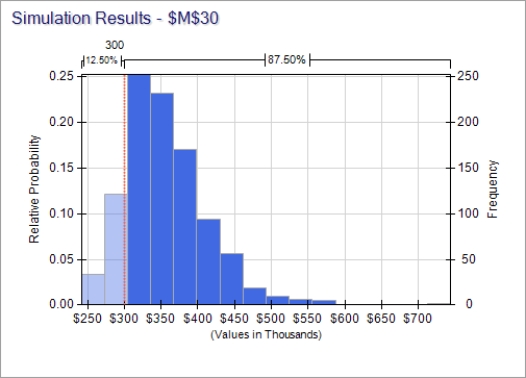 (a)What will be the expected value (mean)of Patrick's nest egg at year 10? (b)What will be the standard deviation of Patrick's nest egg at year 10? (c)What is the probability that the total nest egg at year 10 will be at least $300,000? d).The returns of each fund are allowed to accumulate (i.e.,are re-investe)
(a)What will be the expected value (mean)of Patrick's nest egg at year 10? (b)What will be the standard deviation of Patrick's nest egg at year 10? (c)What is the probability that the total nest egg at year 10 will be at least $300,000? d).The returns of each fund are allowed to accumulate (i.e.,are re-investe)
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents