A second order differential equation can be arranged to the form 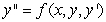 , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is
, and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is 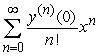 , one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What is the coefficient of x4 in the Taylor polynomial expansion of the solution to the equation
, one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What is the coefficient of x4 in the Taylor polynomial expansion of the solution to the equation 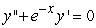 if the initial conditions are
if the initial conditions are 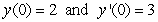 ?
?
A) 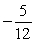
B) 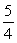
C) 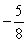
D) 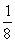
Correct Answer:
Verified
Q28: Solve the initial value problem 
Q29: A series circuit has an 0.3 henry
Q30: Find the recurrence relation for the general
Q31: Identify the radius of convergence of the
Q32: A series circuit has a 0.25 henry
Q33: For a pendulum of weight 4 pounds,
Q34: Identify the radius of convergence of the
Q35: Solve the initial value problem 
Q36: Identify the pair of graphs that correspond
Q37: A series circuit has a 0.15 henry
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents