The Population of Two Species Is Modeled by the System $$\left\{ \begin{array} { l } \frac { d x } { d t } = 2 x - x y \\\frac { d y } { d t } = - 4 y + x y\end{array} \right.$$

The population of two species is modeled by the system of equations $$\left\{ \begin{array} { l } \frac { d x } { d t } = 2 x - x y \\\frac { d y } { d t } = - 4 y + x y\end{array} \right.$$ .(a) Find an expression for $\frac { d y } { d x }$ .(b) A possible direction field for the differential equation in part (a) is given below: 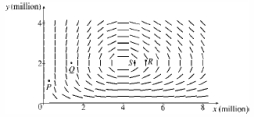Use this graph to sketch a phase portrait with each of P, Q, R, and S as an initial condition. Describe the behavior of the trajectories near the nonzero equilibrium solutions.(c) Graph x and y as function of t. What happens to the population of the two species as the time t increases without bound?