Solved

The Following Data Show the Demand for an Airline Ticket

Question 62

Multiple Choice

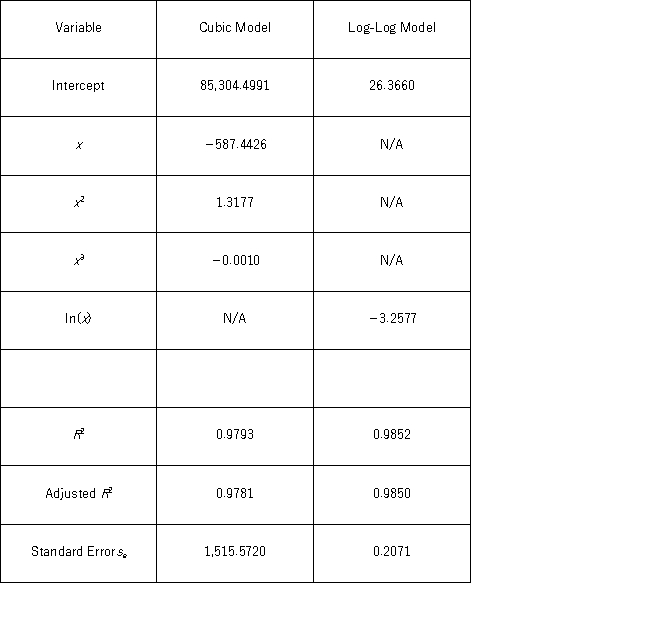The following data show the demand for an airline ticket dependent on the price of this ticket. The following data show the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models,Demand = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Price<sup>2 </sup>+ β<sub>3</sub>Price<sup>3 </sup>+ ε and ln(Demand) = β<sub>0</sub> + β<sub>1</sub>ln(Price) + ε,the following regression results are available. Assuming that the sample correlation coefficient between Demand and = exp(26.3660 - 3.2577 ln(Price) + (0.2071) <sup>2</sup>/2) is 0.956,what is the percentage of variations in Demand explained by the log-log regression equation? A) 98.52% B) 98.50% C) 91.39% D) 97.93% For the assumed cubic and log-log regression models,Demand = β0 + β1Price + β2Price2 + β3Price3 + ε and ln(Demand) = β0 + β1ln(Price) + ε,the following regression results are available. The following data show the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models,Demand = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Price<sup>2 </sup>+ β<sub>3</sub>Price<sup>3 </sup>+ ε and ln(Demand) = β<sub>0</sub> + β<sub>1</sub>ln(Price) + ε,the following regression results are available. Assuming that the sample correlation coefficient between Demand and = exp(26.3660 - 3.2577 ln(Price) + (0.2071) <sup>2</sup>/2) is 0.956,what is the percentage of variations in Demand explained by the log-log regression equation? A) 98.52% B) 98.50% C) 91.39% D) 97.93% Assuming that the sample correlation coefficient between Demand and The following data show the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models,Demand = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Price<sup>2 </sup>+ β<sub>3</sub>Price<sup>3 </sup>+ ε and ln(Demand) = β<sub>0</sub> + β<sub>1</sub>ln(Price) + ε,the following regression results are available. Assuming that the sample correlation coefficient between Demand and = exp(26.3660 - 3.2577 ln(Price) + (0.2071) <sup>2</sup>/2) is 0.956,what is the percentage of variations in Demand explained by the log-log regression equation? A) 98.52% B) 98.50% C) 91.39% D) 97.93% = exp(26.3660 - 3.2577 ln(Price) + (0.2071) 2/2) is 0.956,what is the percentage of variations in Demand explained by the log-log regression equation?


A) 98.52%
B) 98.50%
C) 91.39%
D) 97.93%

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q43: For the exponential model ln(y) = β0

Q58: A model in which the response variable

Q59: The following Excel scatterplot with the fitted

Q60: A model with one explanatory variable being

Q61: The following data,with the corresponding Excel scatterplot,show

Q63: The following data show the demand for

Q64: The following data,with the corresponding Excel scatterplot,show

Q65: The following data show the demand for

Q66: The logarithmic and log-log models,y = β0

Q67: The following data show the demand for

Unlock this Answer For Free Now!

View this answer and more for free by performing one of the following actions

qr-code

Scan the QR code to install the App and get 2 free unlocks

upload documents

Unlock quizzes for free by uploading documents