During the last few days before a presidential election,there is a frenzy of voting intention surveys.On a given day,quite often there are conflicting results from three major polls.
(a)Think of each of these polls as reporting the fraction of successes (1s)of a Bernoulli random variable Y,where the probability of success is Pr(Y = 1)= p.Let 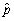 be the fraction of successes in the sample and assume that this estimator is normally distributed with a mean of p and a variance of
be the fraction of successes in the sample and assume that this estimator is normally distributed with a mean of p and a variance of  .Why are the results for all polls different,even though they are taken on the same day?
.Why are the results for all polls different,even though they are taken on the same day?
(b)Given the estimator of the variance of 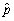 ,
, 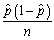 ,construct a 95% confidence interval for
,construct a 95% confidence interval for 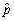 .For which value of
.For which value of 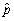 is the standard deviation the largest? What value does it take in the case of a maximum
is the standard deviation the largest? What value does it take in the case of a maximum 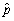 ?
?
(c)When the results from the polls are reported,you are told,typically in the small print,that the "margin of error" is plus or minus two percentage points.Using the approximation of 1.96 ≈ 2,and assuming,"conservatively," the maximum standard deviation derived in (b),what sample size is required to add and subtract ("margin of error")two percentage points from the point estimate?
(d)What sample size would you need to halve the margin of error?
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q37: The power of the test
A)is the probability
Q38: A low correlation coefficient implies that
A)the line
Q39: The t-statistic is defined as follows:
A)
Q40: The following statement about the sample correlation
Q41: Your textbook states that when you test
Q42: At the Stock and Watson (http://www.pearsonhighered.com/stock_watson)website go
Q44: Let Y be a Bernoulli random variable
Q46: Let p be the success probability of
Q53: The accompanying table lists the height
Q61: Consider two estimators: one which is biased
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents