Let Y be a Bernoulli random variable with success probability Pr(Y = 1)= p,and let Y1,... ,Yn be i.i.d.draws from this distribution.Let  be the fraction of successes (1s)in this sample.In large samples,the distribution of
be the fraction of successes (1s)in this sample.In large samples,the distribution of 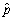 will be approximately normal,i.e. ,
will be approximately normal,i.e. , 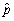 is approximately distributed N(p,
is approximately distributed N(p, 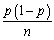 ).Now let X be the number of successes and n the sample size.In a sample of 10 voters (n=10),if there are six who vote for candidate A,then X = 6.Relate X,the number of success,to
).Now let X be the number of successes and n the sample size.In a sample of 10 voters (n=10),if there are six who vote for candidate A,then X = 6.Relate X,the number of success,to 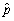 ,the success proportion,or fraction of successes.Next,using your knowledge of linear transformations,derive the distribution of X.
,the success proportion,or fraction of successes.Next,using your knowledge of linear transformations,derive the distribution of X.
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q39: The t-statistic is defined as follows:
A)
Q40: The following statement about the sample correlation
Q41: Your textbook states that when you test
Q42: At the Stock and Watson (http://www.pearsonhighered.com/stock_watson)website go
Q42: During the last few days before a
Q46: Let p be the success probability of
Q48: The development office and the registrar have
Q48: A manufacturer claims that a certain brand
Q53: The accompanying table lists the height
Q61: Consider two estimators: one which is biased
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents