Consistency for the sample average 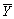 can be defined as follows,with the exception of
can be defined as follows,with the exception of
A) 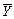 converges in probability to
converges in probability to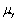 .
.
B) 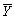 has the smallest variance of all estimators.
has the smallest variance of all estimators.
C) 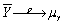 .
.
D) the probability of 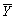 being in the range
being in the range ± c becomes arbitrarily close to one as n increases for any constant c > 0.
± c becomes arbitrarily close to one as n increases for any constant c > 0.
Correct Answer:
Verified
Q23: You have read about the so-called catch-up
Q24: To infer the political tendencies of the
Q26: Probabilities and relative frequencies are related in
Q29: The sample average is a random variable
Q30: The variance of Q31: Math and verbal SAT scores are each Q31: Assume that you assign the following subjective![]()
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents