Consider the model Yi - β1Xi + ui,where the Xi and ui the are mutually independent i.i.d.random variables with finite fourth moment and E(ui)= 0.
(a)Let 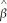 1 denote the OLS estimator of β1.Show that
1 denote the OLS estimator of β1.Show that 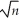 (
( 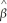 1- β1)=
1- β1)= 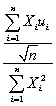 .
.
(b)What is the mean and the variance of 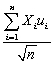 ? Assuming that the Central Limit Theorem holds,what is its limiting distribution?
? Assuming that the Central Limit Theorem holds,what is its limiting distribution?
(c)Deduce the limiting distribution of 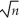 (
( 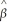 1 - β1)? State what theorems are necessary for your deduction.
1 - β1)? State what theorems are necessary for your deduction.
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q23: The WLS estimator is called infeasible WLS
Q33: "One should never bother with WLS. Using
Q39: The large-sample distribution of Q40: Assume that var(ui|Xi)= θ0+θ1 Q41: Consider estimating a consumption function from a Q44: Consider the simple regression model Yi = Q45: (Requires Appendix material)If the Gauss-Markov conditions hold,then Q46: (Requires Appendix material)Your textbook considers various distributions Q47: Your textbook states that an implication of Q49: (Requires Appendix material)State and prove the Cauchy-Schwarz![]()
![]()
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents