Consider the simple regression model Yi = β0 + β1Xi + ui where Xi > 0 for all i,and the conditional variance is var(ui  Xi)= θX
Xi)= θX 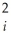 where θ is a known constant with θ > 0.
where θ is a known constant with θ > 0.
(a)Write the weighted regression as  i = β0
i = β0 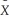 0i + β1
0i + β1 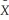 1i +
1i +  i.How would you construct
i.How would you construct  i,
i, 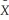 0i and
0i and 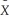 1i?
1i?
(b)Prove that the variance of is  i homoskedastic.
i homoskedastic.
(c)Which coefficient is the intercept in the modified regression model? Which is the slope?
(d)When interpreting the regression results,which of the two equations should you use,the original or the modified model?
Correct Answer:
Verified
Q39: The large-sample distribution of Q40: Assume that var(ui|Xi)= θ0+θ1 Q41: Consider estimating a consumption function from a Q42: Consider the model Yi - β1Xi + Q45: (Requires Appendix material)If the Gauss-Markov conditions hold,then Q46: (Requires Appendix material)Your textbook considers various distributions Q47: Your textbook states that an implication of Q48: (Requires Appendix material)This question requires you to Q49: (Requires Appendix material)State and prove the Cauchy-Schwarz Q49: For this question you may assume that![]()
![]()
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents