Solve Using Cramer's Rule $W _ { 1 }$ And $W _ { 2 }$

Solve using Cramer's Rule.
-Linear systems occur in the design of roof trusses for new homes and buildings. The simplest type of roof truss is a triangle. The truss shown in the figure is used to frame roofs of small buildings. If a 109-pound force is applied at the peak of the truss, then the forces or weights $W _ { 1 }$ and $W _ { 2 }$ exerted parallel to each rafter of the truss are determined by the following linear system of equations. Solve the system to find 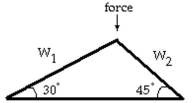$W _ { 1 }$ and $W _ { 2 }$ .

$W _ { 1 } + \sqrt { 2 } W _ { 2 } = 218$

$\sqrt { 3 } W _ { 1 } - \sqrt { 2 } W _ { 2 } = 0$

A) $W _ { 1 } = 109 \mathrm { lb } ; \mathrm { W } _ { 2 } = 133.5 \mathrm { lb }$
B) $\mathrm { W } _ { 1 } = 79.79 \mathrm { lb } ; \mathrm { W } _ { 2 } = 97.73 \mathrm { lb }$
C) $\mathrm { W } _ { 1 } = 39.9 \mathrm { lb } ; \mathrm { W } _ { 2 } = 48.86 \mathrm { lb }$
D) $\mathrm { W } _ { 1 } = 97.73 \mathrm { lb } ; \mathrm { W } _ { 2 } = 79.79 \mathrm { lb }$