The following MINITAB output presents a multiple regression equatior $\hat { y }$=b₀+b₁x₁+b₂x₂+b₃x₃+b₄x₄ The regression equation is $$\mathrm { Y } = 4.7712 + 0.2662 \mathrm { X } 1 + 1.2710 \mathrm { X } 2 - 1.1349 \mathrm { X } 3 - 1.8545 \mathrm { X } 4$$ $\begin{array}{lllll} \text { Predictor } & \text { Coef } & \text { SE Coef } & \text { T } & \mathrm{P} \ \text { Constant } & 4.7712 & 0.7648 & 0.92800 & 0.3280 \ \mathrm{X} 1 & 0.2662 & 0.8036 & -0.93740 & 0.3570 \ \mathrm{X} 2 & 1.2710 & 0.8451 & 1.74170 & 0.0830 \ \mathrm{X} 3 & -1.1349 & 0.6318 & -2.94990 & 0.0080 \ \mathrm{X} 4 & -1.8545 & 0.6753 & 3.27200 & 0.0020 \end{array}$ $\text { Analysis of Variance }$ $\begin{array}{lccccc} \text { Source } & \text { DF } & \text { SS } & \text { MS } & \text { F } & \text { P } \ \text { Regression } & 4 & 624.2 & 156.1 & 9.8797 & 0.003 \ \text { Residual Error } & 40 & 633.7 & 15.8 & & \ \text { Total } & 44 & 1,257.9 & & & \ \hline \end{array}$ 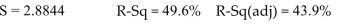It is desired to drop one of the explanatory variables. Which of the following is the most appropriate action? A) Drop x₄, then see whether R² increases B) Drop x₁, then see whether R² increases C) Drop x₄, then see whether adjusted R² increases D) Drop x₁, then see whether adjusted R² increases

Question

Quizplus · Accepted Answer

To determine which variable to drop, we need to check if dropping a variable would increase the adjusted R-squared value. Adjusted R-squared is preferred over regular R-squared for selecting the model with the best fit when comparing models with different numbers of variables. In this case, we should drop x₁ and compare the adjusted R-squared value with and without it. If the adjusted R-squared value increases after dropping x₁, then it is the most appropriate variable to drop. Therefore, the best choice is D, drop x₁, then see whether adjusted R² increases.

The Following MINITAB Output Presents a Multiple Regression Equatior y^\hat { y }y^​

The Following MINITAB Output Presents a Multiple Regression Equatior $\hat { y }$