The following MINITAB output presents a multiple regression equation .
The regression equation is
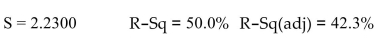
b3x3 What percentage of the variation in y is explained by the model?
A) 50.0%
B) 42.3%
C) 0.3%
D) 7.7396%
Correct Answer:
Verified
Q40: The following MINITAB output presents a
Q41: The following MINITAB output presents a
Q42: The following MINITAB output presents a
Q43: Construct the multiple regression sequence
Q44: The following table lists values measured
Q46: The following MINITAB output presents a
Q47: The following MINITAB output presents a
Q48: The following MINITAB output presents a
Q49: The following MINITAB output presents a
Q50: The following MINITAB output presents a
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents