Solve the problem. Use the critical-value approach.
-A machine that fills soda bottles is supposed to fill them to a mean volume of 16.2 fluid ounces. A random sample of 20 filled bottles produced the following volumes in fluid ounces: 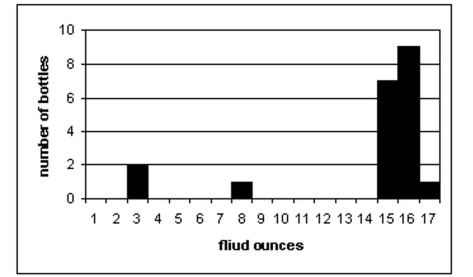
Using technology, perform the following hypothesis test: at the 5% significance level,determine Whether the fill volume is less than the supposed value. Comment on the appropriateness of the Test.
A) Test statistic: ; Critical value: .
Since the test statistic is greater than the critical value, do not reject the null hypothesis . There is insufficient evidence to conclude that the fill volume is below oz. The conclusion is on sound statistical ground.
B) Test statistic: ; Critical value: .
Since the test statistic is less than the critical value, do not reject the null hypothesis .
There is insufficient evidence to conclude that the fill volume is below oz. However, the data exhibits 3 outliers. Elimination of these outliers may alter the conclusion.
C) Test statistic: ; Critical value; .
Since the test statistic is greater than the critical value, do not reject the null hypothesis . There is insufficient evidence to conclude that the fill volume is below
oz. However, the data exhibits 3 outliers. Elimination of these outliers may alter the conclusion.
D) Test statistic: ; Critical value: .
Since the test statistic is less than the critical value, reject the null hypothesis .
There is sufficient evidence to conclude that the fill volume is below . However, the data exhibits 3 outliers. Elimination of these outliers may alter the conclusion.
Correct Answer:
Verified
Q13: Construct a graph portraying the decision
Q14: Two graphical displays are given for
Q15: Solve the problem. Use the critical-value approach.
-A
Q16: Construct a graph portraying the decision
Q17: Solve the problem. Use the critical-value
Q19: Provide an appropriate response.
-Suppose that you want
Q20: A hypothesis test for a population
Q21: Two graphical displays are given for a
Q22: In 1995, the mean math SAT
Q23: Construct a graph portraying the decision criterion
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents