The radial portion of the de Broglie wavefunction for an electron in the ground state of the hydrogen atom is 1s(r) = 1/() 1/2 exp(-r/a0) where a0 is the Bohr radius.The probability of finding the electron is: 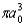
A) 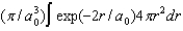
B) 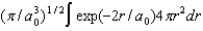
C) 
D) 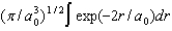
E) 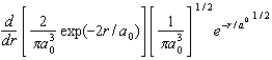
Correct Answer:
Verified
Q2: Suppose Bohr had chosen the potential energy
Q5: Of the following states, 5s, 3p, 4f,
Q8: The probability density of a particle at
Q9: For the following allowed transitions, which photon
Q11: An energy of 13.6 eV is needed
Q13: In a shell of the hydrogen atom
Q14: The energy needed to remove an electron
Q15: An electron in a hydrogen atom makes
Q15: The K, L, M symbols represent values
Q16: The number of states in the He+
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents