Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold.
(a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0.
(b)Show that the r-period ahead forecast E( 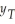 +r
+r 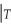 )=
)= 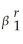
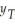 .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of
.If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of 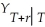 for large r?
for large r?
(c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E(  +r
+r 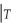 )= 0.5
)= 0.5  .Show that in the present case this is given by r = -
.Show that in the present case this is given by r = - 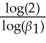 .
.
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q32: The BIC is a statistic
A)commonly used to
Q41: You have collected data for real GDP
Q43: Find data for real GDP (Yt)for the
Q44: (Requires Appendix material): Show that the AR(1)process
Q45: Consider the AR(1)model Yt = β0 +
Q46: Consider the following model
Yt = α0 +
Q46: You want to determine whether or not
Q47: The following two graphs give you a
Q48: (Requires Appendix material)The long-run,stationary state solution of
Q49: You have decided to use the Dickey
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents